Blog do Enem: simplificado como deve ser |
| Inequação modular: propriedades modulares Posted: 14 Jul 2016 05:08 PM PDT Nesta aula, você poderá relembrar o módulo de um número real para que na sequência, sejam apresentadas as propriedades do módulo de um número real, ferramentas importantes para a resolução de uma inequação modular.Módulo de um Número realSabe aquele eterno otimista que só vê o lado positivo das coisas? Então, o módulo é desse jeito!!! Brincadeiras à parte, o módulo ou valor absoluto de um número real x é representado por |x|, que lemos: módulo de x.
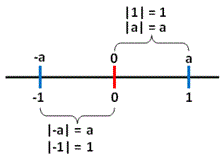
Se x for um número real positivo o módulo de x será o próprio x. Se x for um número real negativo o módulo de x será o oposto de x, ou seja, será -x, resultando portanto em um valor positivo. Apenas sendo x igual a 0, o módulo de x também será 0. Conceituando geometricamente o módulo de um númeroEm termos geométricos o módulo de um número real representa a distância deste número à origem de uma reta real. Na reta desta figura o ponto 0 representa a sua Origem. Cada ponto nesta reta é um número real. Como podemos observar, 3 tanto é a distância do ponto -3 até a origem,quanto é a distância do ponto 3também até a origem. A distância dos pontos em questão é igual a 3 nos dois casos, não importando se o ponto está à direita ou à esquerda da origem. O valor absoluto ou módulo de -3 é igual a 3, assim como o módulo de 3 também o é. Para entender o estudo da inequação modular é necessário compreender as propriedades do módulo e das desigualdades. Portanto, unindo essas duas propriedades, é possível estudar as desigualdades envolvendo números modulares, ou seja, a inequação modular. Propriedades do módulo de um número real
Contudo, iremos estudar desigualdades envolvendo números modulares, consistindo, então, nas inequações modulares. Inequações modularesUma inequação modular é um tipo de inequação que contém um valor absoluto. Um valor absoluto mede a distância que determinado valor tem em relação ao ponto 0 – por exemplo, |x| mede a distância do ponto x até o zero. As inequações modulares têm aplicação em simetrias, limites simétricos ou condições de contorno. Entenda e resolva esse tipo de inequação com alguns passos simples de avaliação ou transformação:
Confira a aula selecionada no link abaixo para ampliar seus conhecimentos!
Os textos e exemplos acima foram preparados pela professora Jaceli Eccher para o Blog do Enem. Jaceli é formada em Matemática habilitação Licenciatura pela Universidade Federal de Santa Catarina com Especialização no ensino de Ciências pelo Instituto Federal de Santa Catarina. Facebook: https://www.facebook.com/JacelieccherO post Inequação modular: propriedades modulares apareceu primeiro em Blog do Enem. |
| Definição de módulo e função modular Posted: 14 Jul 2016 06:57 AM PDT Neste post você aprenderá a definição de módulo de um número real e a definição de função modular, assim como o seu gráfico e as equações modulares e suas resoluções.Módulo de um Número realPodemos dizer que módulo é o mesmo que distância de um número real ao número zero, pois o módulo de número real surgiu da necessidade de medir a distância de um número negativo ao zero. Assim, podemos dizer que o módulo de um número real irá seguir duas opções:
A representação de um módulo ou valor absoluto de um número real é feito por duas barras paralelas. Veja o resumo da definição de módulo de um número real abaixo: |x| = x, se x ≥ 0 Função ModularDependendo dos valores de x uma função f pode ser definida por duas ou mais sentenças. Como exemplo podemos ter uma função de IR em IR definida por:
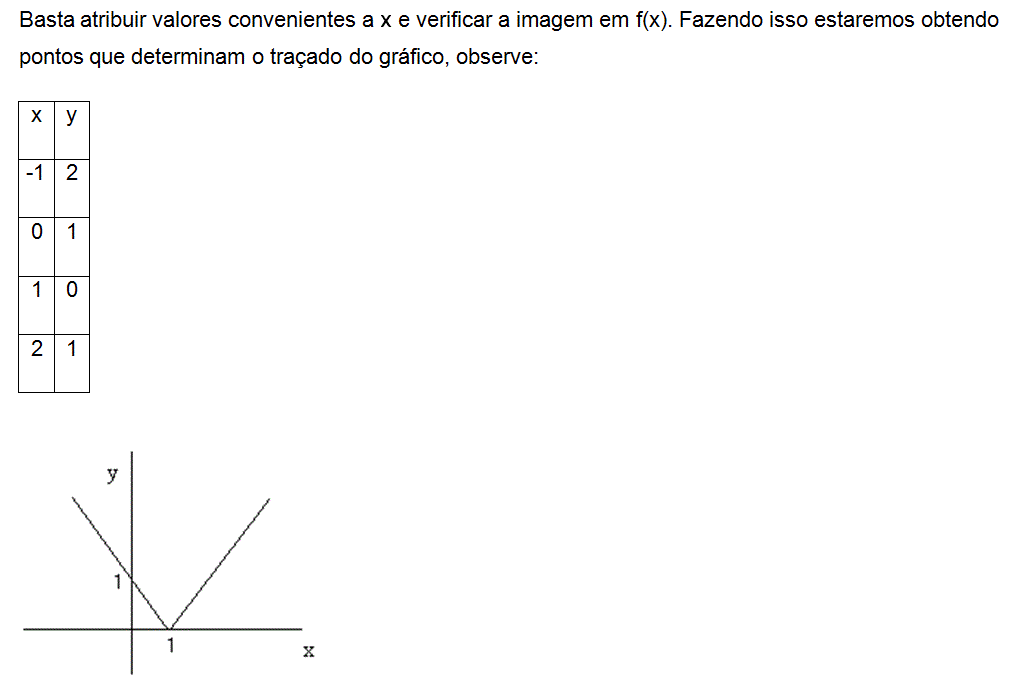
A função modular apresenta a característica de valor absoluto, isto é, o que está em modulo é considerado em valor absoluto e consequentemente, sem sinal. Define-se módulo ou valor absoluto de x e indica-se por | x |.
Equações ModularesNas equações modulares, usa-se a mesma ideia, isto é, o que está em módulo ou é positivo ou é negativo, e isto pode ser alterado multiplicando-se a equação negativa por –1. Ex 1.: | x – 2 | = 3
A aula abaixo apresenta um pouco mais sobre equações modulares. Clique e assista! |
| You are subscribed to email updates from Blog do Enem. To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google Inc., 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States | |






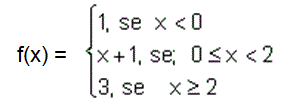
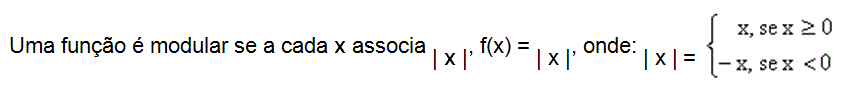






0 comentários:
Postar um comentário