Blog do Enem: simplificado como deve ser |
- UEMG – Notas de Corte do Enem na Univ. Estadual de Minas Gerais
- Configuração dos Elétrons: veja Química Enem com a Khan Academy
- Combustão: veja a reação química que pega fogo!
- Teorema de Tales – Aula de Matemática Enem
| UEMG – Notas de Corte do Enem na Univ. Estadual de Minas Gerais Posted: 25 Jun 2016 09:35 PM PDT É uma boa estudar na UFMG – Uma grande vantagem da Universidade Estadual de Minas Gerais é a grande rede que a instituição tem de campus espalhados pela capital, Belo Horizonte, e no interior do Estado. Você pode estudar em Poços de Caldas, Diamantina, Ibirité, Passos, Campanha, Juiz de Fora, Claudio, Carangola, Frutal e outas cidades. Veja todas as notas de corte Sisu 2016 na UFMG. Nas carreiras mais disputadas para entrar na Universidade Estadual de Minas Gerais os candidatos tiveram que remar muito para vencer as barreiras das notas de corte Sisu 2016 na UEMG. O curso de graduação com a peneira mais apurada na seleção dos candidatos foi Medicina, na cidade de Passos, com 784,80 pontos pelo Enem nas notas de corte Sisu 2016 na UEMG. Campeão geral. Em seguida, também com notas muito altas, vieram os seguintes cursos de graduação nas principais disputas: Design Gráfico, em Belo Horizonte, no turno matutino, com 763,90 pontos; Direito, na cidade de Passos, com 743,90 pontos; Design Gráfico, turno da noite, em Belo Horizonte, com 743,53 pontos; e, o curso de graduação em Direito, no campus da cidade de Frutal, com 739,62 pontos nas notas de corte Sisu 2016 na UEMG. Curso Enem GratuitoVocê quer mandar bem no próximo Enem? Mude a sua vida com uma boa nota nas provas objetivas e na redação com aulas, dicas, exercícios e simulados do Curso Pré-Enem 2016. Todas as matérias para você revisar de graça 24 horas por dia. Veja aqui o Curso Enem Online.  As menores notas de corte do Enem na UEMGPara quem não conseguiu pontuação média no Enem acima dos pontos também deu para entrar em diversos cursos de graduação na Universidade Estadual de Minas Gerais. Por exemplo, na cidade de a disputa pelas vagas de Produção Sucroalcooleira ficou com a menor das notas de corte Sisu 2016 na UEMG, com apenas 564,27 pontos. O mesmo curso, na cidade de Frutal, exigiu 586,27 pontos para entrar. Em seguida, também com baixa pontuação, ficaram os seguintes cursos de graduação da UEMG: Curso Alimentos, em Frutal, com 587,55 pontos. Curso de Pedagogia, na unidade Carangola, com 601,35 pontos; e o curso de graduação em Química, em Ituiutaba, com 604,48 pontos de Nota de Corte do Enem na UEMG.
Tabela completa das Notas de Corte do Enem na UEMG – Sisu 2016
O post UEMG – Notas de Corte do Enem na Univ. Estadual de Minas Gerais apareceu primeiro em Blog do Enem. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Configuração dos Elétrons: veja Química Enem com a Khan Academy Posted: 25 Jun 2016 07:00 PM PDT Não vacile. É hora de rever um conteúdo que cai muito nas provas dos vestibulares e do Enem: a distribuição dos elétrons – ou Distribuição Eletrônica, cai direto, mas é um assunto que confunde muitos alunos na hora das provas. Veja como aprender e se dar bem no Enem.A professora de Química Munique Dias, de Florianópolis, preparou uma super aula para você. Tem a teoria, os exemplos, vídeos da Khan Academy, e uma bateria de exercícios no padrão dos vestibulares e do Enem. Tudo começa nas teorias dos modelos atômicos do filósofo Demócrito; depois, em 1803, com o inglês John Dalton; em seguida Joseph John Thomson em 1897; Arthur Rutherford entre 1908 e 1910; e mais recentemente o Modelo de Niels Bohr, chamado de Bohr-Ruthenberg, e datado de 1913. Se você não estiver em dia com as teorias dos Modelos Atômicos, faça aqui uma revisão da Estrutura do Átomo antes de prosseguir.
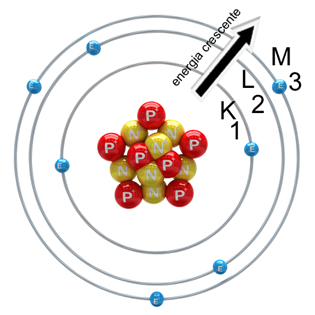
O cientista Niels Bohr propôs em 1913 que os elétrons estavam distribuídos em camadas definidas. A eletrosfera atômica, portanto, era constituída por sete camadas eletrônicas, numeradas de um a sete, -1-2-3-4-5-6-7-, as quais também poderiam ser representadas pelas letras maiúsculas K,L,M,N,O,P e Q. A camada 1 (ou K) era a camada mais próxima do núcleo e de menor energia, e a 7 (ou Q), a mais distante e de menor energia. Ou seja, as camadas não eram ‘apenas camadas’, mas reuniam características e propriedades próprias na eletrosfera. A forma como os elétrons estão distribuídos ao redor do núcleo, em camadas ou níveis de energia, é chamada de Distribuição eletrônica (veja na imagem acima). Você sabe fazer a distribuição dos elétrons na eletrosfera? Veja com a gente para chegar lá…Para você fazer a distribuição dos elétrons nas camadas do átomo, você deve seguir algumas "regras", não gosta de decorar regras? Nem a gente! Por isso o nosso blog preparou para você um breve roteiro, assim você nunca mais vai esquecer:
Entendeu? Que tal um exemplo? Vamos fazer a distribuição eletrônica do potássio (K)? Resolução: O número atômico do potássio é 19. Como o potássio encontra-se no seu estado fundamental ou neutro, temos que o número atômico é igual ao número de elétrons. Então distribuindo os elétrons nas camadas eletrônicas, e respeitando o número máximo de elétrons para cada camada temos que: 19K = K=2; L=8; M=8; N=1 Obs: A última camada eletrônica de um átomo comporta no máximo, oito elétrons. Assim, se a última camada contiver um número de elétrons superior a 8 e inferior a 18, deve-se deixar 8 nessa e passar para a próxima. Aula Gratuita sobre o Modelo Atômico de Niels BohrAntes de continuar esta aula sobre a a distribuição dos Elétrons no átomo, precisamos lembrar o modelo atômico Bohr. Vamos relembrar? Sabe como? Assistindo um resumo sobre o modelo atômico de Bohr com o professor Marcos Mariano:
Vamos lembrar como é feita a distribuição dos elétrons nos subníveis (configuração eletrônica)? Os subníveis são preenchidos em ordem crescente de energia (ordem energética). Linus Pauling descobriu que a energia dos subníveis cresce na ordem: Diagrama de Linus Pauling Vamos ver o exemplo do oxigênio: Oxigênio (O) Z = 8 → 1s2 2s2 2p4 (estado fundamental). Linnus Carl Pauling (1901-1994) foi um químico quântico e bioquímico dos Estados Unidos. Foi pioneiro na aplicação da Mecânica Quântica em química e, em 1994, ganhou o Nobel de Química pelo seu trabalho relativo à natureza das ligações químicas. Pauling recebeu o Nobel da Paz de 1962, pela sua campanha contra os testes nucleares e é a única personalidade a ter recebido dois Prêmios Nobel não compartilhados. Vamos aprender mais um pouco? Não desista agora!! Assista este outro vídeo da Khan Academy sobre os orbitais, e mande super bem nas questões sobre elétrons nas provas dos vestibulares ou do Enem. Os textos e exemplos de apresentação desta aula foram preparados pela professora Munique Dias para o Blog do Enem. Munique é formada em química pela UFSC, tem mestrado e atualmente cursa o doutorado em Engenharia. Química, também pela UFSC. Facebook: https://www.facebook.com/MuniqueDias . O post Configuração dos Elétrons: veja Química Enem com a Khan Academy apareceu primeiro em Blog do Enem. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Combustão: veja a reação química que pega fogo! Posted: 25 Jun 2016 07:39 AM PDT A queima de materiais é uma reação química. Você sabe qual? – Se você respondeu ‘Combustão’, acertou de primeira. É isso mesmo, a queima de materiais é uma reação química de combustão. Cai nas provas dos vestibulares e também no Enem. Vamos relembrar? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Teorema de Tales – Aula de Matemática Enem Posted: 25 Jun 2016 06:30 AM PDT O Teorema de Tales – Cálculos geométricos envolvendo ‘Proporção’. É incrível a lógica envolvida. É simples e dá resultados extraordinários. Veja!O Teorema de Tales é uma importante ferramenta utilizada há muitos e muitos séculos na determinação de medidas utilizando a proporcionalidade. Reza a lenda que a construção das antigas Pirâmides no Egito, por exemplo, só foi possível a partir dos cálculos derivados do Teorema de Tales. A origem do Teorema está com o filósofo e matemático grego Tales de Mileto, que viveu entre 623 a.C e 548 a.C. Para compreender a dimensão destas proposições, leia a frase seguinte com muita calma, e articulando o seu pensamento com a imagem associada: "Se duas ou mais retas paralelas forem cortadas por um feixe retas transversais, formam-se nas transversais segmentos correspondentes proporcionais". É a essência para compreender o Teorema de Tales. Observe agora a figura., e vá aplicando o raciocínio da proposição: As características que dão o fundamento para o Teorema de Tales: Observe novamente na figura acima os seguintes aspectos:
De acordo com Tales podemos construir a seguinte proporção:A B A’ B’ = B C B’ C’ = A C A’ C’ Dica 1 – Preparado para enfrentar a prova de Matemática Enem? Revise os conceitos relacionados aos ângulos e suas classificações para gabaritar na prova – http://blogdoenem.com.br/angulos-matematica-geometria-enem/ Aula Gratuita sobre o Teorema de TalesSaiba mais sobre o Teorema de Tales com esta aula do canal Me Salva: Desafios sobre o Teorema de Tales:Considerando o Teorema de Tales, nas figuras, a // b // c, calcule o valor de x: Questão 1 a) 10 b) 10,5 c) 11 d) 12,5 e) 13 Questão 2 a) 1 b) 1,5 c) 1,8 d) 2 e) 2,5 Questão 3 a) 10 b) 12 c) 13 d) 14 e) 15 Dica 2 – Estude para a prova de Matemática Enem com esta aula sobre Razões e proporcionalidade – http://blogdoenem.com.br/razoes-proporcoes-matematica-enem/Questão 4 A figura abaixo nos mostra duas avenidas que partem de um mesmo ponto A e cortam duas ruas paralelas. Na primeira avenida, os quarteirões determinados pelas ruas paralelas tem 80 m e 90 m de comprimento, respectivamente. Na segunda avenida, um dos quarteirões determinados mede 60 m. Qual o comprimento do outro quarteirão ? a) 67,5 b) 69 c) 70,5 d) 72 e) 75 Dica 3 – Fique preparado para a prova de Matemática do Enem revisando o conteúdo com esta aula completa sobre intervalos em R – http://blogdoenem.com.br/intervalos-r-matematica-enem/Questão 5 Na figura abaixo, um garoto está em cima de um banco. Qual é a altura desse garoto que projeta uma sombra de 1,2 m, sabendo que o banco de 30 cm projeta uma sombra de 40 cm ? a) 75 cm b) 80 cm c) 0,9 m d) 1,10 m e) 1,2 m Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender! O post Teorema de Tales – Aula de Matemática Enem apareceu primeiro em Blog do Enem. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| You are subscribed to email updates from Blog do Enem. To stop receiving these emails, you may unsubscribe now. | Email delivery powered by Google |
| Google Inc., 1600 Amphitheatre Parkway, Mountain View, CA 94043, United States | |




 Esses três fatores compõem o
Esses três fatores compõem o 

0 comentários:
Postar um comentário